
In general, any two angles that add to 90 o are called complementary. When the non-common rays of adjacent angles are perpendicular, their measures add to 90 o: These angles are supplementary, but not a linear pair: Their measures just have to add to 180 o. This word is less specific than linear pair in that the angles do not have to be adjacent. The word supplementary is given when two angles add to 180 o. When adjacent angles add to, the two non-common rays form a straight angle, and the two angles are called a linear pair: That is, the bisector of an angle is a ray that spits it into two equal pieces. (Adjacent are two angles that share a common ray.) When adjacent angles are equal, the common ray is the bisector of the larger angle. Thus, a precise definition of angle bisector is:ĭefinition: Ray is the bisector of if it is interior to the angle and :Īs with the Segment Addition Postulate for segments, we have an Angle Addition Postulate:Īngle Addition Postulate: If is interior to, then : This is similar to saying that the midpoint of a segment is a point on that segment (or "between" its endpoints) that cuts it into two equal segments. The bisector of an angle is a ray interior to the angle that cuts it in half. The bisector of an angle is a ray that cuts that angle into two equal angles: The standard is to place an "m" before the name of the angle:Īs with segments, angles can also be bisected. If we want to focus on their measures, then we need another notation. If they have the same measure (degrees), we should say they are congruent and again use an equals-sign with a tilde over it.
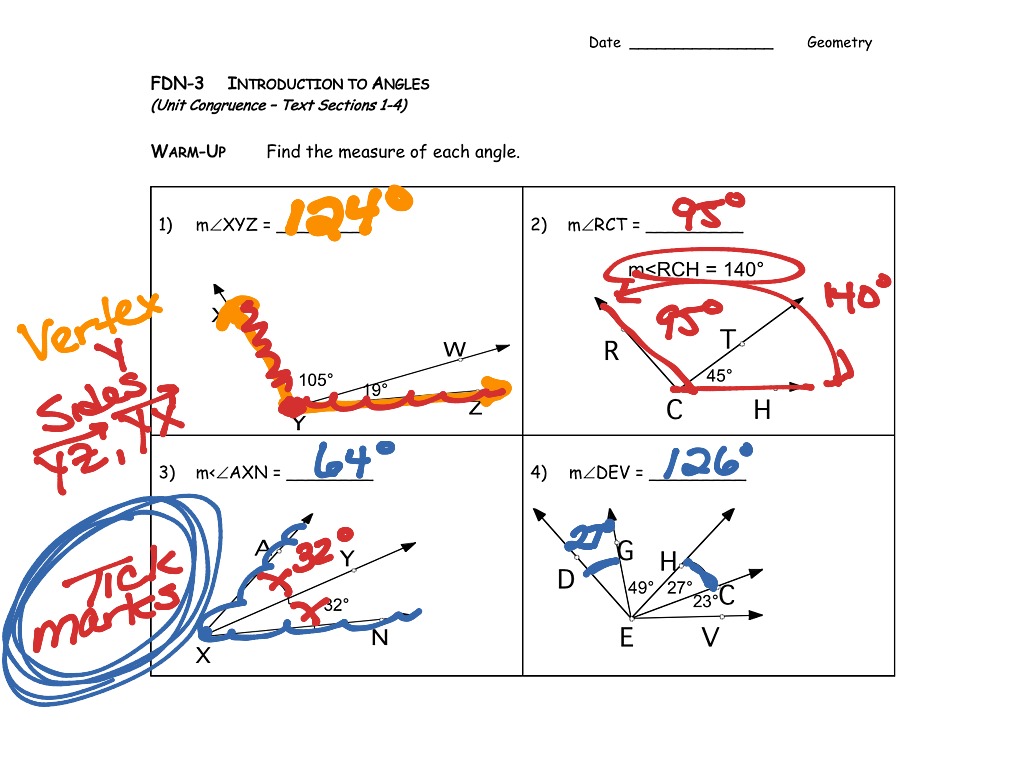
Axiom 3.32 (A2: Angle addition postulate) If D lies in the interior of ABC, then mABD + m. In geometry, we say two physical objects are congruent when they have the same measure, and we use an equals-sign with a "tilde" over it:Īs we learned before, angles are notated with a slanting L. Remark: this definition is only valid in Euclidean geometry. When two segments have the same length we say they are "equal." When we want to distinguish between a segment and its length, we use a bar over its endpoints for the physical object and no bar for the length.


 0 kommentar(er)
0 kommentar(er)
